Função quadrática completa e incompleta
Gráfico da Função quadrática
O gráfico da função quadrática é uma parábola, cuja concavidade é determinada de acordo com o valor de a. Se a > 0, a concavidade da parábola estará voltada para cima e se a < 0, a concavidade da parábola estará voltada para baixo.
Mais sobre o gráfico
- Se b > 0 a parábola intersecta o eixo Y subindo.
- Se b = 0 a parábola intersecta o eixo Y “reta”.
- Se b < 0 a parábola intersecta o eixo Y descendo.
- c é o ponto em que a parábola vai intersectar o eixo Y.
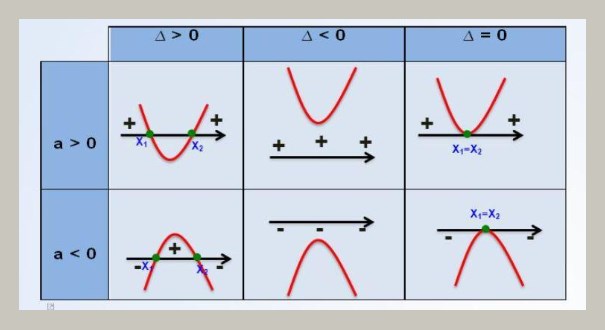
- Se Δ > 0 a parábola corta o eixo X duas vezes.
- Se Δ = 0 a parábola tangencia o eixo X.
- Se Δ < 0 a parábola não encostará no eixo X.
Raízes e Vértice
Dois conceitos estão relacionados à concavidade da parábola: as raízes (pontos onde o gráfico intercepta o eixo x) e o vértice (ponto de máximo ou mínimo a função). As raízes podem ser calculadas pela fórmula de Bháskara ou outros métodos. Lembrando que, as funções quadráticas possuem apenas duas raízes.
Em relação ao vértice, na função de primeiro grau é possível traçar o gráfico a partir de dois pontos. Contudo, isso não acontece na função de segundo grau, pois é necessário conhecer mais que dois pontos.
A partir do valor do = b² – 4ac, sabemos que:
• Se > 0, a função possui duas raízes reais distintas e a parábola intercepta o eixo x em dois pontos diferentes;
• Se = 0, a função possui duas raízes reais iguais e a parábola é tangente ao eixo x;
• Se < 0, a função não possui raízes reais e a parábola não intercepta o eixo x;
Exemplo:
Encontre as raízes (ou zeros) da função f(x) = x2 – 5x + 6.
Solução:
Sendo
a = 1
b = – 5
c = 6
Substituindo esses valores na fórmula de Bhaskara, temos:
Portanto, as raízes são 2 e 3.

Uma resposta para “Resumo sobre Função quadrática”