Neste tipo de função, o número a é chamado de coeficiente de x e representa a taxa de crescimento ou taxa de variação da função. Já o número b é chamado de termo constante.
Gráfico:
O gráfico de uma função polinomial do 1º grau é uma reta oblíqua aos eixos X e Y. Desta forma, para construirmos seu gráfico basta encontrarmos pontos que satisfaçam a função.
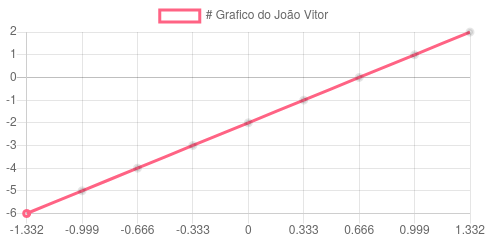
Exemplo: Construa o gráfico da função f (x) = 2x + 3.
Resolução :
Para construir o gráfico desta função, vamos atribuir valores arbitrários para x, substituir na equação e calcular o valor correspondente para a f (x).
Sendo assim, iremos calcular a função para os valores de x iguais a: – 2, – 1, 0, 1 e 2. Substituindo esses valores na função, temos:
f (- 2) = 2. (- 2) + 3 = – 4 + 3 = – 1
f (- 1) = 2 . (- 1) + 3 = – 2 + 3 = 1
f (0) = 2 . 0 + 3 = 3
f (1) = 2 . 1 + 3 = 5
f (2) = 2 . 2 + 3 = 7
Os pontos escolhidos e o gráfico da f (x) são apresentados na imagem abaixo:
No exemplo, utilizamos vários pontos para construir o gráfico, entretanto, para definir uma reta bastam dois pontos.
Para facilitar os cálculos podemos, por exemplo, escolher os pontos (0,y) e (x,0). Nestes pontos, a reta da função corta o eixo X e Y respectivamente (esses pontos são chamados de interceptos).
Interceptos:
Os interceptos são os pontos em que a reta intercepta os eixos X e Y (ou seja os pontos em que o valor de X ou o valor de Y será igual a zero) onde:
intercepto de X =
Intercepto de Y: (também chamado de raiz da função)
No caso da função mostrada acima os interceptos seriam: (0,3) e (-1,5, 0)
Coeficiente Linear e Angular
Como o gráfico de uma função afim é uma reta, o coeficiente a de x é também chamado de coeficiente angular. Esse valor representa a inclinação da reta em relação ao eixo X
O termo constante b é chamado de coeficiente linear e representa o ponto onde a reta corta o eixo Y. Pois sendo x = 0, temos:
y = a.0 + b ⇒ y = b
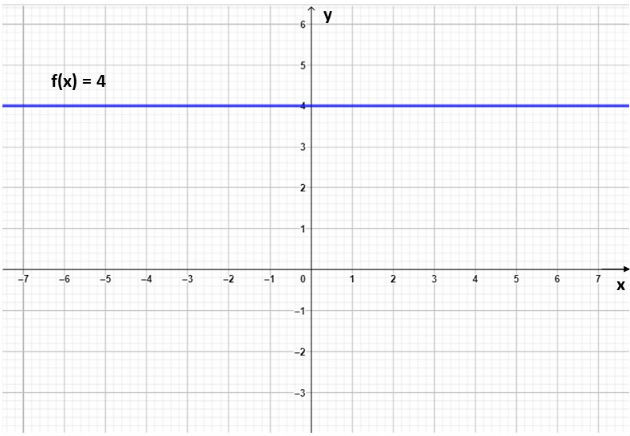
Quando uma função afim apresentar o coeficiente angular igual a zero (a = 0) a função será chamada de constante. Neste caso, o seu gráfico será uma reta paralela ao eixo X.
Abaixo representamos o gráfico da função constante f (x) = 4:
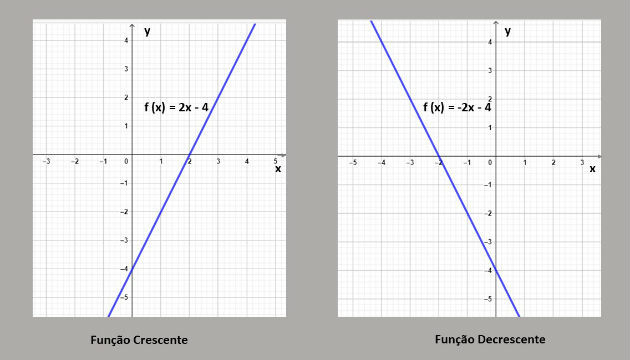
Função crescente ou decrescente
O que determina se uma função é crescene ou decrescente é o “a”
se a > 0 = função crescente
se a < 0 = função decrescente
Por exemplo, a função 2x – 4 é crescente, pois a = 2 (valor positivo). Entretanto, a função – 2x + – 4 é decrescente visto que a = – 2 (negativo). Essas funções estão representadas nos gráficos abaixo:
Exemplo:
Dada a função f(x) = 3x -2 determine:
a) os coeficientes angular e linear.
b) se é crescente ou decrescente
c) os interceptos.
d) o gráfico dessa função.
Resolução:
a) Coeficiente angular = a
a = 3
Coeficiente angular = 3
Coeficiente linear = b
b = -2
Coeficiente linear = -2
b) é crescente pois a > 0
c)
intercepto de x =
intercepto de y =
d)