Definição hexágono regular

Hexágono é um polígono que possui seis lados delimitados por segmentados de reta.

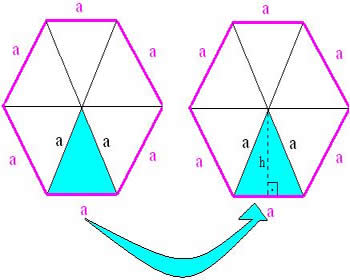
O hexágono regular é aquele que é formado pela junção de seis triângulos equiláteros, por essa razão todos os lados possuem a mesma medida e seus ângulos internos são de 120º. Portanto, a área do hexágono é seis vezes a área de um triângulo equilátero que o compõe.

Perímetro e área:

O perímetro de um hexágono regular é dado pela fórmula:

$p=6l$

Onde:

p = perímetro

l = medida dos lados

Para calcular a área é usada a seguinte fórmula:

$a=\frac{3l^{2}\sqrt{3}}{2}$

a = área

l = medida dos lados

Veja a seguir os passos para chegar á essa fórmula:

Como dito anteriormente a área de um hexágono regular é dada pela área de seis triânguloss equiláteros e para a área de um triângulo é usada a seguinte fórmula:

$a=\frac{b\cdot h}{2}$

b = base

h = altura

Para descobrir a altura de um triângulo equilátero é necessário traçar um segmento no meio de um de seus lados dividindo ele em dois triângulos retângulos, desta forma:

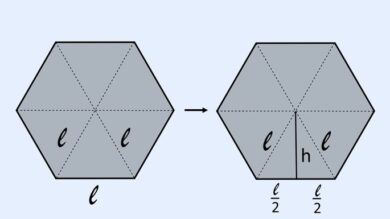
Como temos triângulos retângulos podemos utilizar o Teorema de Pitágoras para calcular a altura desse triângulo da seguinte forma:

$l^{2}=h^{2}+\left (\frac{l}{2} \right )^{2}$

$h^{2}=l^{2}-\frac{l^{2}}{4}$

$h^{2}=\frac{3l^{2}}{4}$

$h=\frac{\sqrt{3}}{2}l$

Substituindo na fórmula da área do triângulo:

$a=\frac{l\cdot l\cdot \frac{\sqrt{3}}{2}}{2}$

fazendo as multiplicações obtemos que:

$a=\frac{l^{2}\sqrt{3}}{4}$

Porém essa é a área de apenas um dos triângulos equiláteros e o hexágono é formado por seis desses portanto:

$a_h=\frac{6l^{2}\sqrt{3}}{4}$

fazendo a simplificação:

$a_h=\frac{3l^{2}\sqrt{3}}{2}$

Apótema:

O apótema nada mais é do que a altura do triângulo equilátero que nós encontramos anteriormente e ele também pode ser usado para calcular a área com a seguinte fórmula:

$a=\frac{p\cdot \alpha }{2}$

Onde:

a = área

p = perímetro

α = apótema

Quando um hexágono regular está inscrito em uma circunferência, os seis vértices da figura dividem a circunferência em seis partes iguais. Neste caso, o raio da circunferência (r) coincide com o lado do hexágono (l), pois formam um triângulo equilátero $incremento OAB$ . Como vemos na figura abaixo:

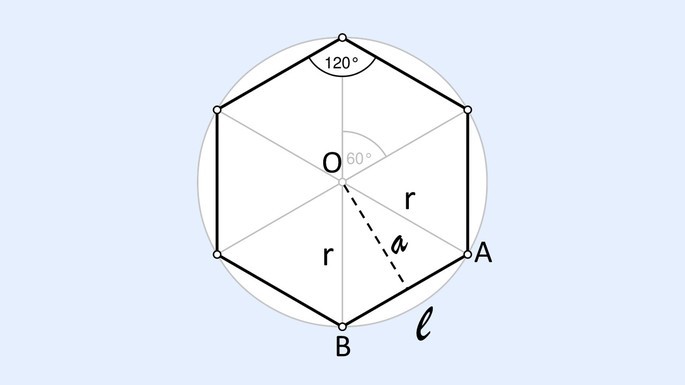
Sendo , aplicamos o Teorema de Pitágoras e encontramos a fórmula para calcular o apótema da seguinte forma:

$r^{2}=\alpha ^{2}+\frac{r^{2}}{4}$

$\alpha ^{2}=r^{2}-\frac{r^{2}}{4}$

$\alpha ^{2}=\frac{3r^{2}}{4}$

$\alpha=\frac{r\cdot \sqrt{3}}{2}$

Exemplo:

Para fazer um hexágono Pedro cortou uma cartolina e com uma régua mediu que todos os lados tinham 10 cm. Qual o perímetro, a área e o apótema do hexágono que Pedro criou?

Resolução:

perímetro: $p=10\cdot 6=60cm$

área: $a=\frac{300\sqrt{3}}{2}=150\sqrt{3}cm^{2}$

apótema: $\alpha=\frac{10\sqrt{3}}{2}=5\sqrt{3}cm$

Aqui no site existe um post feito para calcular o perímetro, a área e o apótema do hexágono regular, basta você inserir a medida do lado que ele te entregará todas as outras, clique no botão abaixo para conhecê-lo:

9 de março de 20219 de março de 2021

Propriedades do hexágono regular

INSTRUÇÕES DE PREENCHIMENTO:

1- Preencha o campo do lado e clique em calcular e pronto, você terá o perímetro, a área e o apótema desse hexágono.

2- Não se preocupe com a unidade da medida, apenas lembre-se que todas as medidas estarão na mesma unidade, (exemplo: se o raio for em metros, todas as outras medidas serão em metros).

3- ATENÇÃO esses cálculos se aplicam apenas em hexágonos regulares (que possuem todos os lados do mesmo tamanho), para hexágonos irregulares são outras fórmulas.

fórmulas:

Perímetro: ${\color{DarkGreen} p=6l}$

Área: ${\color{DarkGreen} a=\frac{3l^{2}\sqrt{3}}{2}}$

Apótema: ${\color{DarkGreen} \alpha =\frac{l\sqrt{3}}{2}}$

Onde:

l = Lados

p = Perímetro

a = Área

α = Apótema

Digite a medida dos lados e depois clique em calcular

l =

27 de novembro de 202028 de novembro de 2020

Definição losango

Um losango é um polígono que possui quatro lados congruentes. Sendo assim, o losango é formado por segmentos de reta, chamados de lados do polígono, que se encontram apenas pelas extremidades. Esses segmentos de reta acabam formando uma figura fechada e seus lados não se cruzam em momento algum.

Para ser losango, além de possuir todos os lados congruentes, a figura geométrica precisa ter exatamente quatro lados. Isso classifica o losango como quadrilátero e também são classificados como paralelogramos pois seus lados opostos são paralelos.

Elementos e propriedades

Lados: São os segmentos de reta que limitam o polígono;
Vértices: são os pontos de encontro entre dois lados;
Ângulos internos: ângulos entre dois lados na região interna do polígono;
Diagonais: Segmentos de reta que ligam dois vértices e que não são lados. São também definidos como segmentos de reta que ligam dois vértices não consecutivos.

Como os losangos são paralelos seus ângulos e lados opostos são congruentes, a soma de seus ângulos internos totaliza 360º e as diagonais se cruzam em seus pontos médios.

Perímetro e área:

Perímetro: soma de todos os lados, dado pela fórmula:

$P = 4l$

Onde:

P = perímetro

l = lados do losango

Área: a superfície da figura, dada pela fórmula: $A=\frac{(D\cdot d)}{2}$

Onde:

A = área

D = diagonal maior

d = diagonal menor

Exemplos:

1 -A prefeitura de uma cidade gasta R$ 33,00 por metro quadrado de grama plantada. Sabendo que uma praça, que possui formato de losango, foi totalmente revestida com essa mesma grama e que as diagonais dessa praça medem 18 m e 22 m, responda: quanto a prefeitura gastou nessa obra?

Para responder essa questão temos que calcular a área desse losango e multiplicar pelo preço da grama, nesse caso:

$A=\frac{(22\cdot 18)}{2}$

$A=\frac{396}{2}=198m^{2}$

$198\cdot 33=R\$6534,00$

Portanto esse será o preço da grama

Aqui no site temos um programa para calcular o perímetro e a área do losango, onde você só precisa informar o tamanho das diagonais e o programa te informará a medida dos lados. o perímetro e a área, clique no botão abaixo para conhecê-lo: