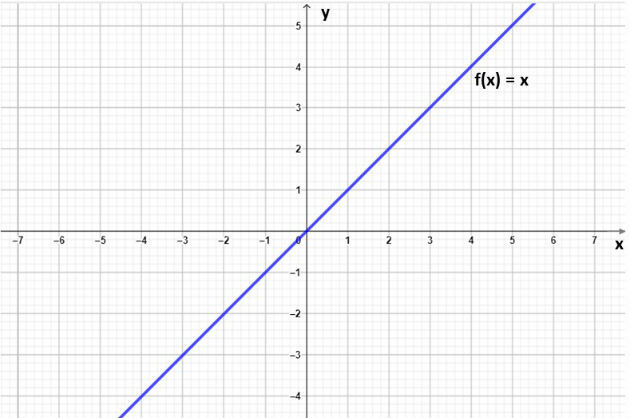
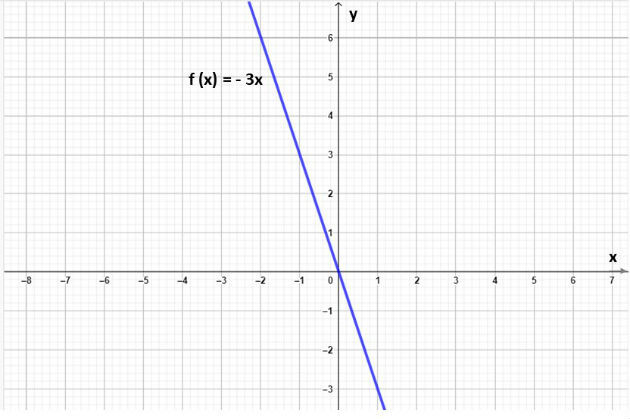
Definição função afim
Neste tipo de função, o número a é chamado de coeficiente de x e representa a taxa de crescimento ou taxa de variação da função. Já o número b é chamado de termo constante.
Gráfico:
O gráfico de uma função polinomial do 1º grau é uma reta oblíqua aos eixos X e Y. Desta forma, para construirmos seu gráfico basta encontrarmos pontos que satisfaçam a função.
Exemplo: Construa o gráfico da função f (x) = 2x + 3.
Resolução :
Para construir o gráfico desta função, vamos atribuir valores arbitrários para x, substituir na equação e calcular o valor correspondente para a f (x).
Sendo assim, iremos calcular a função para os valores de x iguais a: – 2, – 1, 0, 1 e 2. Substituindo esses valores na função, temos:
f (- 2) = 2. (- 2) + 3 = – 4 + 3 = – 1
f (- 1) = 2 . (- 1) + 3 = – 2 + 3 = 1
f (0) = 2 . 0 + 3 = 3
f (1) = 2 . 1 + 3 = 5
f (2) = 2 . 2 + 3 = 7
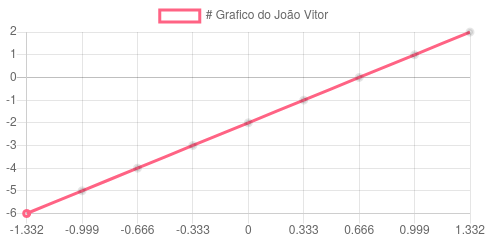
Os pontos escolhidos e o gráfico da f (x) são apresentados na imagem abaixo:
No exemplo, utilizamos vários pontos para construir o gráfico, entretanto, para definir uma reta bastam dois pontos.
Para facilitar os cálculos podemos, por exemplo, escolher os pontos (0,y) e (x,0). Nestes pontos, a reta da função corta o eixo X e Y respectivamente (esses pontos são chamados de interceptos).
Interceptos:
Os interceptos são os pontos em que a reta intercepta os eixos X e Y (ou seja os pontos em que o valor de X ou o valor de Y será igual a zero) onde:
intercepto de X =
Intercepto de Y: (também chamado de raiz da função)
No caso da função mostrada acima os interceptos seriam: (0,3) e (-1,5, 0)
Coeficiente Linear e Angular
Como o gráfico de uma função afim é uma reta, o coeficiente a de x é também chamado de coeficiente angular. Esse valor representa a inclinação da reta em relação ao eixo X
O termo constante b é chamado de coeficiente linear e representa o ponto onde a reta corta o eixo Y. Pois sendo x = 0, temos:
y = a.0 + b ⇒ y = b
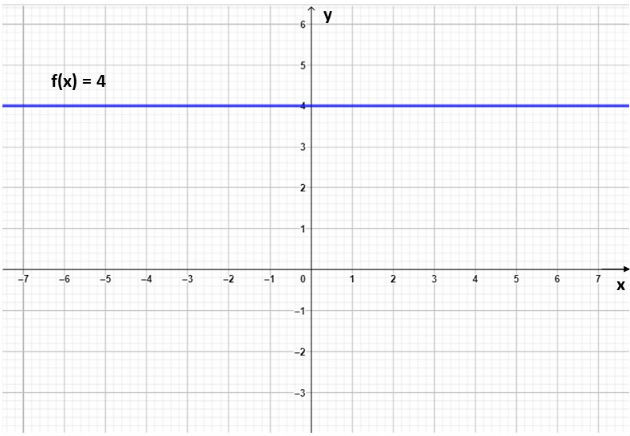
Quando uma função afim apresentar o coeficiente angular igual a zero (a = 0) a função será chamada de constante. Neste caso, o seu gráfico será uma reta paralela ao eixo X.
Abaixo representamos o gráfico da função constante f (x) = 4:
Função crescente ou decrescente
O que determina se uma função é crescene ou decrescente é o “a”
se a > 0 = função crescente
se a < 0 = função decrescente
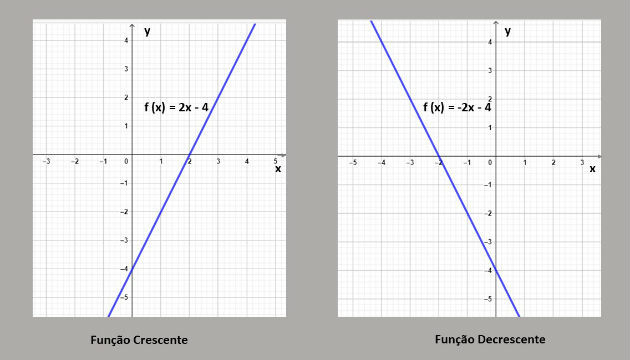
Por exemplo, a função 2x – 4 é crescente, pois a = 2 (valor positivo). Entretanto, a função – 2x + – 4 é decrescente visto que a = – 2 (negativo). Essas funções estão representadas nos gráficos abaixo:
Exemplo:
Dada a função f(x) = 3x -2 determine:
a) os coeficientes angular e linear.
b) se é crescente ou decrescente
c) os interceptos.
d) o gráfico dessa função.
Resolução:
a) Coeficiente angular = a
a = 3
Coeficiente angular = 3
Coeficiente linear = b
b = -2
Coeficiente linear = -2
b) é crescente pois a > 0
c)
intercepto de x =
intercepto de y =
d)
Agora que você aprendeu tudo que tal começar a calcular suas funções afim?
Definição Juro simples e Juro composto
Juro simples
Juros simples é um acréscimo calculado sobre o valor inicial de um aplicação financeira ou de uma compra feita a crédito, por exemplo.
O valor inicial de uma dívida, empréstimo ou investimento é chamado de capital. A esse valor é aplicada uma correção, chamada de taxa de juros, que é expressa em porcentagem.
Os juros são calculados considerando o período de tempo em que o capital ficou aplicado ou emprestado.
Exemplo
Um cliente de uma loja pretende comprar uma televisão, que custa 1000 reais à vista, em 5 parcelas iguais. Sabendo que a loja cobra uma taxa de juros de 6% ao mês nas compras a prazo, qual o valor de cada parcela e o valor total que o cliente irá pagar?
Quando compramos algo parcelado, os juros determinam o valor final que iremos pagar. Assim, se compramos uma televisão a prazo iremos pagar um valor corrigido pela taxa cobrada.
Ao parcelamos esse valor em cinco meses, se não houvesse juros, pagaríamos 200 reais por mês (1000 divididos por 5). Mas foi acrescido 6 % a esse valor, então temos:
![]()
Desta forma, teremos um acréscimo de R$ 12 ao mês, ou seja, cada prestação será de R$ 212. Isso significa que, no final, pagaremos R$ 60 a mais do valor inicial.
Logo, o valor total da televisão a prazo é de R$1060.
Fórmula e como calcular
A fórmula para calcular os juros simples é expressa por:
J = C . i . t
Onde,
J: juros
C: capital
i: taxa de juros. Para substituir na fórmula, a taxa deverá estar escrita na forma de número decimal. Para isso, basta dividir o valor dado por 100.
t: tempo. A taxa de juros e o tempo devem se referir à mesma unidade de tempo.
Podemos ainda calcular o montante, que é o valor total recebido ou devido, ao final do período de tempo. Esse valor é a soma dos juros com valor inicial (capital).
Sua fórmula será:
M = C + J → M = C + C . i . t
Juro composto
Os juros compostos são recorrentes nas relações comerciais, nas compras parceladas a longo prazo, nos investimentos, nos empréstimos e até mesmo no simples atraso do pagamento de contas. O juros pode ser um aliado ou um vilão. É importante dominar os fatores que influenciam o seu cálculo, que são o capital, a taxa de juros, o tempo e o montante.
Ao comparar o juros composto com o juros simples, precisamos entender que o primeiro é calculado sempre sobre o valor do exercício anterior, já o segundo é calculado sempre em cima do valor inicial. O juros composto terá maior crescimento com o passar do tempo, em comparação com o juros simples.
Fórmula e como calcular
A fórmula para calcular montante com juro composto é dada por é expressa por:
Onde,
M: montante
C: capital
i: taxa de juros. Para substituir na fórmula, a taxa deverá estar escrita na forma de número decimal. Para isso, basta dividir o valor dado por 100.
t: tempo. A taxa de juros e o tempo devem se referir à mesma unidade de tempo.
Para calcular os juros basta a fórmula é:
J=M-C
Exemplo
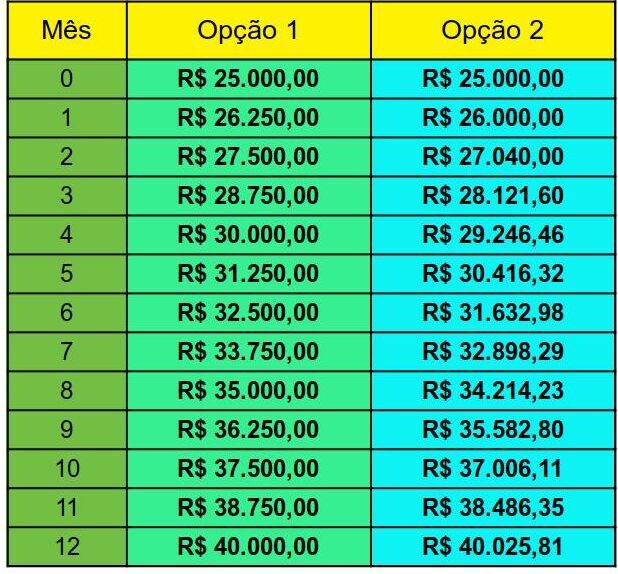
Para investir R$25.000, Maria cotou duas opções:
opção 1: 5% a.m. a juros simples
opção 2: 4% a.m a juros composto
A partir de quanto tempo a segunda opção é mais vantajosa?
Como vemos na tabela acima até 11 meses é mais vantajoso a opção 1, porém a partir do 12º mês será mais vantajoso optar pela opção 2