definição – Página: 3 – Matemática do João Vitor

20 de novembro de 202024 de novembro de 2020

Definição Teorema de Pitágoras

O teorema de Pitágoras relaciona as medidas dos lados de um triângulo retângulo da seguinte maneira:

Em um triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

O teorema de Pitágoras é muito importante para a Matemática, tendo influenciado outros grandes resultados matemáticos. Veja também uma das demonstrações do teorema e parte da biografia de seu criador.

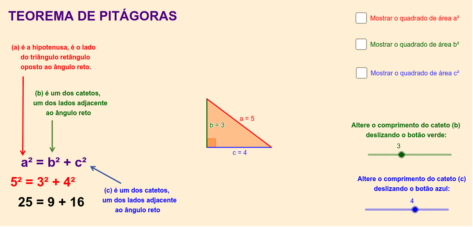
Fórmula

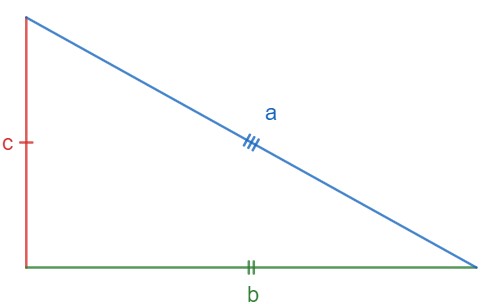
Para aplicação do teorema de Pitágoras, é necessário compreender as nomenclaturas dos lados de um triângulo retângulo. O maior lado do triângulo fica sempre oposto ao maior ângulo, que é o ângulo de 90°. Esse lado recebe o nome de hipotenusa e será representado aqui pela letra a.

Os demais lados do triângulo são chamados de catetos e serão aqui representados pelas letras b e c.

Teorema de Pitágoras e os números irracionais

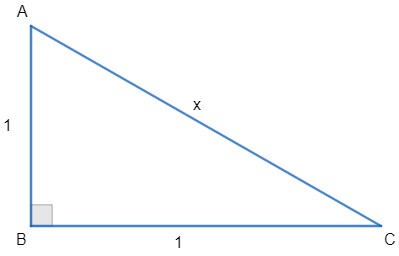
O teorema de Pitágoras trouxe consigo uma nova descoberta. Ao construir um triângulo retângulo em que os catetos são iguais a 1, os matemáticos, na época, depararam-se com um grande desafio, pois, ao encontrar o valor da hipotenusa, um número desconhecido apareceu. Veja:

Cálculo:

$x^{2}=1^{2}+1^{2}$

$x^{2}=2$

$x=\sqrt{2}$

O número encontrado pelos matemáticos da época hoje é chamado de irracional.

Exemplo:

1 – Dois navios A e B partem em sentidos diferentes: o primeiro para o norte e o segundo para o leste, o navio A com velocidade constante de 30 Km/h e o navio B com velocidade constante de 40 Km/h. Qual será a distância entre eles após 6 horas?

Resolução:

Distância do navio A após 6 horas = $30\cdot 6=180Km$

Distância do navio A após 6 horas = $40\cdot 6=240Km$

Como um vai para o Norte e outro para o Leste esses são os nossos catetos, então a distância entre eles será a hipotenusa, ou seja:

$x^{2}=180^{2}+240^{2}$

$x^{2}=32400+57600=90000$

$x=\sqrt{90000}=300Km$

Portanto essa será a distância dos dois navios após 6 horas

Um pintor está pintando um prédio de 15 metros, e sua escada está a 8 metros de distância do prédio formando um ângulo de 90º, qual é a altura da escada desse pintor?

Resolução:

Como a escada está formando um ângulo de 90º então a altura da escada é a hipotenusa e a distância e altura do prédio são os catetos, ou seja:

$x^{2}=15^{2}+8^{2}$

$x^{2}=225+64=289$

$x=\sqrt{289}=17m$

Portanto a altura dessa escada é de 17 metros.

Agora que você sabe tudo isso você pode calcular Teorema de Pitágoras aqui nesse site, clique no botão abaixo:

19 de novembro de 202019 de novembro de 2020

definição de Transformações gasosas

As transformações gasosas consistem em submeter uma massa fixa de um gás a diferentes condições enquanto uma grandeza é mantida constante. Os tipos são:

Transformação isobárica: mudança com pressão constante;
Transformação isotérmica: mudança com temperatura constante;
Transformação isocórica, isométrica ou isovolumétrica: mudança com volume constante.

As grandezas físicas associadas aos gases (pressão, temperatura e volume) são denominadas variáveis de estado e uma transformação sofrida por um gás corresponde a variação de pelo menos duas destas grandezas.

O estudo dos gases foi difundido entre os séculos XVII e XIX por meio de cientistas que desenvolveram as leis dos gases. As leis foram obtidas através da manipulação das grandezas associadas e utilizando um modelo teórico chamado de gás perfeito, criado para estudar o comportamento de substâncias no estado gasoso.

Transformação isobárica

Na transformação isobárica a pressão da massa fixa de um gás é mantida constante, enquanto temperatura e volume variam.

A pressão é uma grandeza que relaciona a aplicação de uma força em determinada área, matematicamente expressa por:

$reto p espaço igual a espaço reto F sobre reto A$

Portanto, no estudo dos gases, a pressão de um gás corresponde à força exercida através dos choques das moléculas nas paredes internas do recipiente.

A transformação isobárica foi estudada, de forma independente, pelos cientistas Jacques Charles (1746-1823) e Louis Joseph Gay-Lussac (1778-1850). A partir de suas observações, foi formulada a Lei de Charles Gay-Lussac:

“Quando a pressão de uma massa fixa de gás é constante, seu volume é diretamente proporcional à sua temperatura absoluta.”

Por exemplo, mantendo a pressão de uma massa de gás constante, ao aumentar ou diminuir a temperatura da amostra, seu volume irá variar na mesma proporção.

Gráfico da transformação isobárica

A seguir, observe o gráfico da transformação isobárica.

Transformação isotérmica

Na transformação isotérmica a temperatura da massa fixa de um gás é mantida constante, enquanto pressão e volume variam.

A temperatura é a grandeza que mede o grau de agitação das moléculas, ou seja, sua energia cinética.

Este tipo de transformação foi estudado por Robert Boyle (1627-1691), que formulou a lei:

“Quando a temperatura de um gás é constante, a pressão do gás é inversamente proporcional ao seu volume.”

Por exemplo, se reduzirmos o volume ocupado por um gás em um recipiente, a pressão exercida por suas moléculas dobrará.

Gráfico da transformação isotérmica

A seguir, observe o gráfico da transformação isotérmica.

Transformação isovolumétrica

Na transformação isovolumétrica, isocórica ou isométrica, o volume de um gás é mantido constante, enquanto pressão e temperatura variam.

O volume de um gás corresponde ao volume do recipiente que ele ocupa, pois as moléculas preenchem todo o espaço disponível.

A transformação com o volume constante foi estudada por Jacques Charles (1746-1823), que postulou o que veio a ser conhecido como Lei de Charles:

“Quando o volume de um gás é mantido constante, sua pressão varia na mesma proporção que a temperatura da amostra.”

Por exemplo, ao dobrar a temperatura de determinado volume de gás, a pressão que o gás exerce nas paredes do recipiente também dobra.

Gráfico da transformação isovolumétrica

A seguir, observe o gráfico da transformação isovolumétrica.

Fórmulas:

As fórmulas para calcular as transformações gasosas são:

Transformação isobárica: $\frac{V_1}{T_1}=\frac{V_2}{T_2}$

Onde:

V = volume do gás

T = temperatura do gás (em K)

Transformação isotérmica: $P_1\cdot V_1=P_2\cdot V_2$

Onde:

P = pressão do gás

V = volume do gás

Transformação isovolumétrica: $\frac{P_1}{T_1}=\frac{P_2}{T_2}$

Onde:

P = pressão do gás

T = temperatura do gás (em K)

Lembre-se: quando estudamos transformações gasosas a temperatura deve estar sempre em Kelvin (K), nunca em Célsius (ºC)

Exemplos:

1 – Certa massa de gás encontra-se com pressão de 2atm e volume de 20 litros, qual será seu volume se mantivermos sua temperatura constante e aumentarmos a pressão para 5atm?

Resolução:

É uma transformação isotérmica então:

$2\cdot 20=5\cdot V_2$

$5 V_2=40$

$V_2=\frac{40}{5}=8l$

2- Certa massa de um gás encontra-se a uma pressão de 900N/M² com uma temperatura de 300K, Se mantivermos constante seu volume e aumentarmos sua temperatura para 400K qual será a pressão desse gás?

Essa é uma transformação isovolumétrica, nesse caso:

$\frac{900}{300}=\frac{P_2}{400}$

$\frac{P_2}{400}=3$

$P_2=3\cdot 400=1200N/m^{2}$

3 – Uma certa massa de gás encontra-se com volume de 0,5m³ à uma temperatura de 200K, se mantivermos a pressão constante e aumentarmos o volume para 1,375m³ , sua temperatura final será de?

Essa é uma transformação isobárica, portanto:

$\frac{0,5}{200}=\frac{1,375}{T_2}$

$0,5T_2=275$

$T_2=\frac{275}{0,5}=550K$

Comece a calcular:

18 de novembro de 202018 de novembro de 2020

Definição dilatação térmica

Dilatação Térmica é a variação que ocorre nas dimensões de um corpo quando submetido a uma variação de temperatura.

De uma maneira geral, os corpos, sejam eles sólidos, líquidos ou gasosos, aumentam suas dimensões quando aumentam sua temperatura.

Dilatação térmica dos sólidos

Um aumento de temperatura faz com que aumente a vibração e o distanciamento entre os átomos que constituem um corpo sólido. Em consequência disso, ocorre um aumento nas suas dimensões.

Dependendo da dilatação mais significativa em uma determinada dimensão (comprimento, largura e profundidade), a dilatação dos sólidos é classificada em: linear, superficial e volumétrica.

Dilatação linear

A dilatação linear leva em consideração a dilatação sofrida por um corpo apenas em uma das suas dimensões. É o que acontece, por exemplo, com um fio, em que o seu comprimento é mais relevante do que a sua espessura,

Para calcular a dilatação linear utilizamos a seguinte fórmula:

$\Delta l=l\cdot \alpha\cdot \Delta \Theta$

Onde,

ΔL: Variação do comprimento (m ou cm)
L_: Comprimento inicial (m ou cm)
α: Coeficiente de dilatação linear (ºC^-1)
Δθ: Variação de temperatura (ºC)

Dilatação superficial

A dilatação superficial leva em consideração a dilatação sofrida por uma determinada superfície. É o que acontece, por exemplo, com uma chapa de metal delgada.

Para calcular a dilatação superficial utilizamos a seguinte fórmula:

$\Delta A=A\cdot \beta \cdot \Delta \Theta$

Onde,

ΔA: Variação da área (m² ou cm²)
A: Área inicial (m² ou cm²)
β: Coeficiente de dilatação superficial (ºC^-1)
Δθ: Variação de temperatura (ºC)

Vale a pena destacar que o coeficiente de dilatação superficial (β) é igual a duas vezes o valor do coeficiente de dilatação linear (α), ou seja:

β = 2 . α

Dilatação volumétrica

A dilatação volumétrica resulta do aumento no volume de um corpo, o que acontece, por exemplo, com uma barra de ouro.

Para calcular a dilatação volumétrica utilizamos a seguinte fórmula:

ΔV = V₀.γ.Δθ

Onde,

ΔV: Variação do volume (m³ ou cm³)
V: Volume inicial (m³ ou cm³)
γ: Coeficiente de dilatação volumétrica (ºC^-1)
Δθ: Variação de temperatura (ºC)

Repare que o coeficiente de dilatação volumétrico (γ) é três vezes maior que coeficiente de dilatação linear (α), ou seja:

γ = 3 . α

Coeficientes de dilatação linear

A dilatação sofrida por um corpo depende do material que o compõe. Desta forma, no cálculo da dilatação é levado em consideração a substância de que o material é feito, através do coeficiente de dilatação linear (α).

Ex: coeficiente de dilatação da porcelana = $3\cdot 10^{-6\, \, \, o}C^{-1}$

Ex: coeficiente de dilatação do chumbo = $27\cdot 10^{-6\, \, \, o}C^{-1}$

Dilatação térmica dos líquidos

Os líquidos, salvo algumas exceções, aumentam de volume quando a sua temperatura aumenta, da mesma forma que os sólidos.

Entretanto, devemos lembrar que os líquidos não apresentam forma própria, adquirindo a forma do recipiente que os contém.

Por isso, para os líquidos, não faz sentido calcularmos, nem a dilatação linear, nem a superficial, só a volumétrica.

Ex: Coeficiente de dilatação da água = $1,3\cdot 10^{-4\, \, \, o}C^{-1}$

Ex: Coeficiente de dilatação da acetona = $14,93\cdot 10^{-4\, \, \, o}C^{-1}$

Tag: definição

Definição Teorema de Pitágoras

Fórmula

Teorema de Pitágoras e os números irracionais

Exemplo:

Agora que você sabe tudo isso você pode calcular Teorema de Pitágoras aqui nesse site, clique no botão abaixo:

definição de Transformações gasosas

Transformação isobárica

Gráfico da transformação isobárica

Transformação isotérmica

Gráfico da transformação isotérmica

Transformação isovolumétrica

Gráfico da transformação isovolumétrica

Fórmulas:

Exemplos:

Comece a calcular:

Definição dilatação térmica

Dilatação térmica dos sólidos

Dilatação linear

Dilatação superficial

Dilatação volumétrica

Coeficientes de dilatação linear

Dilatação térmica dos líquidos

Conheça também: